예전에 일회용 면도기를 사용할 때에는 유혈이 낭자하는 거울 속 얼굴을 자주 봐야 했던 아픈 추억이 있었다. 그러다가 우연한 기회에 써 본 일회용 면도기. 의외로 괜찮다.
그렇게 일회용 면도기를 사용한 지 반 년을 넘고 있는데, 일회용이라고 꼭 한 번만 사용해야 되는 건 아니다. 내 느낌으론 한 일주일까지는 만족스런 품질을 유지하는 것 같다(그렇다고 방심은 금물!). 계산을 한 번 해보자.
면도를 하루에 한 번 한다고 가정하고, 일회용 면도기의 고장률은 지수분포를 따른다고 가정하자. 그리고 일회용 면도기를 일주일(7일) 사용 가능하다고 할 때 1일 사용시까지의 누적고장률은 얼마일까?
그럼 거꾸로, (1-누적고장률)은 뭐라고 부를까? 不누적고장률? 非누적고장률? 未누적고장률? 책을 찾아 보니 '신뢰도'라고 한다.
아무리 일회용 면도기라지만 겨우 한 번 쓰는데 신뢰도가 0.8669라면 조금 낮게 느껴진다. 그래서 1일 사용 시에도 신뢰도가 한 95%까지 되려면(너무 높였나...)
대략 20정도를 목표로 생산한다면, 1일까지의 신뢰도가 95%되겠다. 이를 표로 정리해보면, 내가 일회용 면도기에 요구하는 최저 신뢰도는 약 0.7수준이 된다.
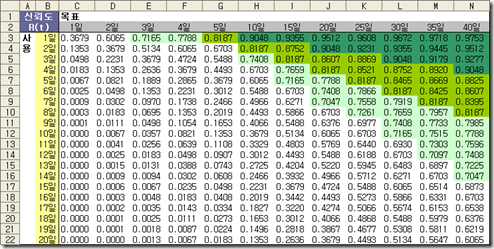
C3 셀에는 이런 수식이 입력되어 있다.
더 높은 신뢰도를 요구하는 소비자도 있을 것이다. 이를 만족시키려면 기대수명을 더 높게 잡아야 하고, 생산 기술도 향상시켜야 하고, 소재 개발도 해야 하고... 다 돈이다 돈.
그런데 일회용 면도기의 고장률이 시간에 따라 일정하지 않다면? 즉 위에서 가정한 지수분포가 아닌 다른 분포, 특히 와이블분포를 따른다고 하면 신뢰도는 달리 나오게 된다. 와이블분포? 고장률이 가속도를 갖는 경우를 말한다.
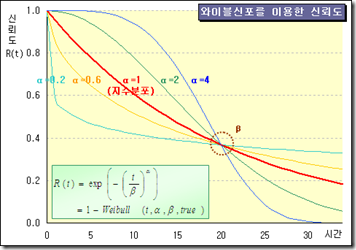
보험이나 산업공학 쪽에서 애용하지 않을까 하는데, 괜히 깝죽대다 쌍권총이 아니라 기관총 맞을 수도 있겠다. 노파심에서 말하지만, 위의 계산 과정은 가정 및 개인 의견이 반영된 것이다. 일회용 면도기의 실제 품질 정보가 반영된 것이 아니니 오해 없기 바란다.





