공공 공사의 경우 예가 15개를 임의로 선정하여 그 중 4개를 무작위로 뽑아 평균을 구한 후, 그 평균보다 크거나 같은 입찰가에서 가장 작은 값을 적격심사 1순위로 선정한다고 하는데, 우리도 간단한 뽑기 한 번 해보자.

1000과 2000 사이의 숫자 중 임의로 15개의 숫자를 위에서처럼 구했다. 그리고 일정한 간격을 나눠 구간을 구분한 후 15개 숫자에 대한 구간별 빈도와 상대빈도(비율)를 구했다.

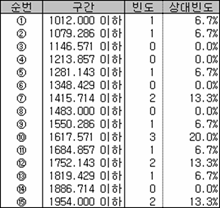
임의로 만들다보니 이빨이 빠진 구간도 있고 많은 구간도 있다. 이제 이 15개의 숫자 중 무작위로 4개를 뽑아내는 경우를 생각해 보자. 15개 중에서 4개를 뽑는 경우의 수는 (15*14*13*12)/(4*3*2*1) = 1,365 가지다. 그래서 1,365 경우의 수 모두에 해당하는 조합을 만들어 구간별 빈도와 상대빈도를 구한다.

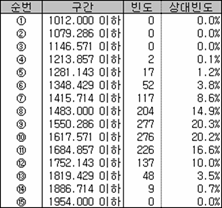
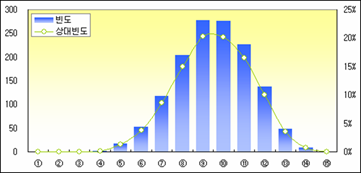
오호~ 자료가 상당히 예쁘게 나왔다. 그리고 4개씩 뽑는 1,365가지 경우의 평균에 평균을 구하면 1550.6 이다. 또 4개씩 뽑는 1365 가지 경우의 분산에 평균을 구하면 280.6²이다.

그런데 임의의 숫자 15개의 평균이 얼마지? 1550.6이다(어라, 똑같네).
그럼 임의의 숫자 15개의 분산은 얼마지? 280.6²이다(어라, 이것도 똑같네. 신기하다).

혹시 우연히 맞은 거 아녀? 이게 우연인지 아닌지 다른 조합을 만들어보자. 위에서는 4개 뽑는 경우를 살펴보았는데 좀 더 확장해서 2개부터 7개까지 뽑는 경우를 가정해서 조합을 만들고 해당 조합별로 얻은 평균의 빈도를 구해 상대빈도(비율)로 나타내 보면,

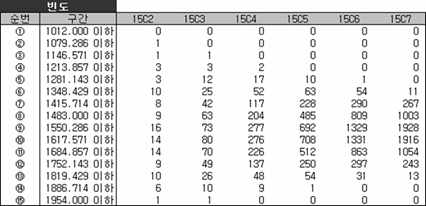
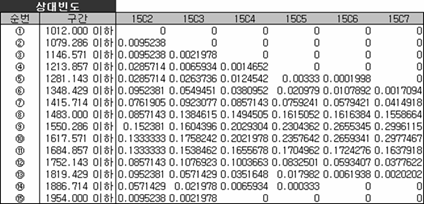
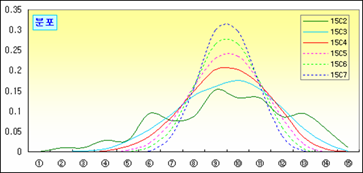
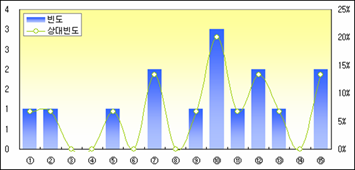
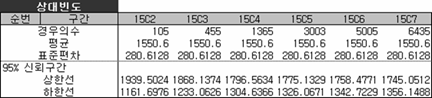
그림을 보니 뽑는 횟수가 커질수록 평균의 분포(비율)는 안정적이고 집중되어 보인다. 그리고 앞에서 처럼 조합별로 평균의 평균과 분산을 각각 구해 정리해 보면,

조합별로 구성된 평균과 분산이 원래 임의의 수 15개를 가지고 구한 평균과 분산과 같다. 이는 표본평균과 표본분산이 불편성과 일치성을 만족하기 때문인데, 이 성질 덕분에 입찰 들어갈 때 일부러 15C4의 조합을 만들고 그 평균을 별도로 구할 필요가 없는 것이다. 물론 지금은 입찰 제도가 바뀌어서 임의의 수 15개를 알 수도 없다.

그런데 위 그림에서 뽑는 횟수가 증가할수록 분포가 익히 보아온 종 모양인 정규분포와 흡사하다.

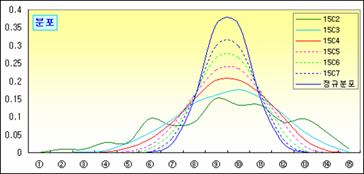
이게 그 유명한 그리고 거의 절대적인 중심극한정리 ^{Central Limit Theroem, CLT}다.

중심극한정리는 원 변수(X)의 평균이 μ이고 분산이 σ²일때, 모집단으로부터 무작위로 n개를 뽑아서(추출) 구한 표본의 평균(X_bar)은 표본크기(n)가 클수록 평균이 μ이고 분산이 σ²/n인 정규분포를 따른다. 즉 표본평균(X_bar) ~ 근사 N(μ, σ²/n)이고, '표본크기(n)'가 크다. 통상적으로 30이상이다(원 변수(X) 분포에 대한 이론이 아니라 표본평균(X_bar)의 분포에 대한 이론인 것에 주의).

즉 원래의 변수가 어떤 분포를 갖는지 몰라도, 표본에서 얻은 평균과 분산을 통해 원 변수의 (모)평균이 어느 위치에 있을 지를 알 수 있다는 거다. 아마도 이 이론이 깨진다면 통계학 책 전부를 불태워야 할 지도 모를 사태가 발생될 것이다.

그런데 뭔가 좀 낯설다. 매우 중요한 정리라며 '평균근사정규정리(가칭)'가 아니라 왜 '중심극한정리'지? 여기에 힌트는 '극한 ^limit'에 있다. 앞서 임의의 수 15개에 대한 조합별 평균과 분산을 가지고 중심극한정리에 대입해 보면,

95% 신뢰구간, 즉 모평균이 위치하고 있을 것으로 추정되는 범위는 뽑는 횟수(표본크기)가 많을수록 수렴하기 때문이다.

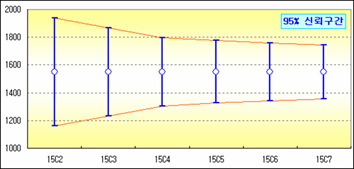
즉 신뢰구간의 폭과 표본크기(n)는 반비례 관계다.

그래서 표본크기가 클수록 좋은데, 그렇다고 큰 게 마냥 좋은 것은 아니다. 예전에도 얘기 했듯이 비표본오차라는 통제 영역을 벗어난 오차가 상존하고 있기 때문인데 그러기에 적절한 표본을 선택해야 되는 것이다.